ALS-XY-Wing
The ALS-XY-Wing rule is a solving technique that uses three Almost Locked Sets.
Make sure you understand the concept of Almost Locked Sets (ALSs) before you proceed.
Contents
How it works
Say we have three Almost Locked Sets A, B and C. Suppose
- A and C share a restricted common Y,
- B and C share a restricted common Z, and
- Y and Z are different digits.
Then for any digit X that is distinct from Y and Z and is a common candidate for A and B, we can eliminate X from any cell that sees all cells belonging to either A or B and having X as a candidate.
Relations to other techniques
Observe that this technique generalizes XY-Wing, and hence the name ALS-XY-Wing. Note that each of the three bivalue cells in the XY-Wing is itself an ALS, hence we can set C as the pivot cell, and the other two pincer cells as A and B respectively.
Recall that the XY-Wing is a chain of length three, and can be generalized to XY-Chain, which is a chain of arbitrarily length. Similarly, we can generalize ALS-XY-Wing to ALS-XY-Chain, which is a chain whose nodes are ALSs instead of single cells.
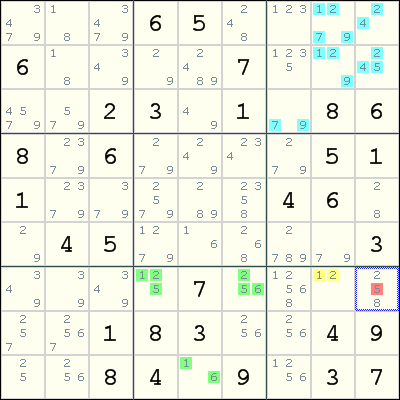
Example
This example is taken from Ron Moore's walkthrough for Ruud's 2007 May 5 Nightmare.
The ALS-XYZ-Wing is constructed as follows:
- The ALS A is the cells colored green in box 8,
- The ALS B is the cells colored light blue in box 3,
- The ALS C is the cell colored yellow in box 9,
- The restricted common Y between A and C is 2, and
- The restricted common Z between B and C is 1.
The cells r7c46 in ALS A and the cell r2c9 in ALS B contain the candidate 5. Since all of r7c46 and r2c9 have a common peer r7c9, we can eliminate 5 from r7c9.
A possible Eureka notation for this elimination is:
(5=24791)ALS:r12c89,r3c8 - (1=2)r7c8 - (216=5)ALS:r7c46,r9c5 => r7c9 <> 5
Note, the reader must check the grid to ensure that r7c9 can see all the 5's in both ALS's and similarly for the links involving digits 1 and 2.
Using the ALS (245)r12c9 and a group node for (2)r12c8 we could also use ALS nodes in an AIC:
(5=42)ALS:r12c9 - (2)r12c8 = (2)r7c8 - (216=5)ALS:r7c46,r9c5 => r7c9 <> 5
which provides greater freedom for the locations of candidates in box 3.
In this example, since the pivot ALS C is a single cell, we can replicate the same elimination using Death Blossom instead.
Notes on notation
Unlike ALS-XZ and XY-Wing, which eliminates the digit Z, the ALS-XY-Wing eliminates the digit X instead. Unfortunately, this inconsistent notation is widely used by the Sudoku community.