Finned Swordfish
A Finned Swordfish is the finned version of a Swordfish. It is a single-digit solving technique.
The formal definition for a Finned Swordfish "in the rows" is:
- When 3 rows only have candidates for digit X in 3 columns and a single box that intersects with at least one of these 3 columns, then we can eliminate all candidates for digit X inside that box, which are located on one of these 3 columns, but not on one of the 3 rows.
Swap the words "rows" and "columns" in this definition for a Finned Swordfish "in the columns".
How it works
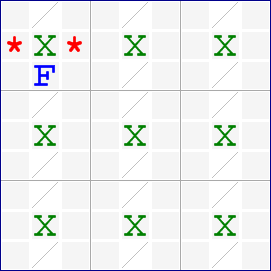
The following fish diagram illustrates how a Finned Swordfish "in the columns" causes eliminations.
Like the basic Swordfish, you do not need a candidate in each cell marked X. In fish techniques, the cells without a candidate are more important.
Example
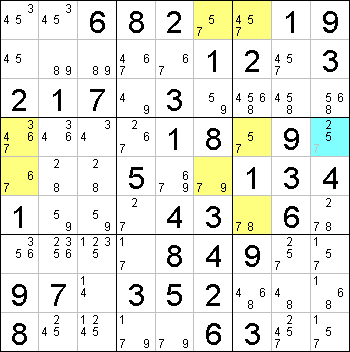
The following example shows a Finned Swordfish "in the columns" for the digit 7 is shown in yellow in the grid, with a fin located at r6c7.
This Finned Swordfish leads to the elimination of 7 from r4c9, which is shown in blue. For clarity, the fish diagram for this example is shown below.
X . . | . . X | X . . / . . | . . / | / . . / . . | . . / | / . . ------+-------+------ X . . | . . X | X * * X . . | . . X | X * * / . . | . . / | F . . ------+-------+------ / . . | . . / | / . . / . . | . . / | / . . / . . | . . / | / . .
An argument for the elimination of 7 from r4c9 is by cases on the fin at r6c7. Case 1 - the fin has value 7: then nothing else in box 6 can have value 7. Case 2 - the fin has value <>7: then the remaining yellow cells form a swordfish-in-columns and so nothing else in rows 1, 4 or 5 can have value 7. Result: common to both of these cases are the deductions that none of r4c8, r4c9, r5c8 or r5c9 can have value 7.