Hidden Single

The Hidden Single is a lot less sinister than its name suggests.

In fact, most of the Sudokus published in newspapers and magazines can be solved by hidden singles only. Together with the Naked Single it belongs to the singles, the most elementary solving techniques.

A Hidden Single is a single candidate remaining for a specific digit in a row, column or box. In Sudoku variants, additional constraints can also produce Hidden Singles.

An alternative term is Pinned Digit.

It may sound like a daunting task, checking 27 houses for each of the 9 digits, thus performing 243 checks, but most players do not check each of these combinations individually. Instead, they use techniques like Scanning and Cross-Hatching to locate the hidden singles.

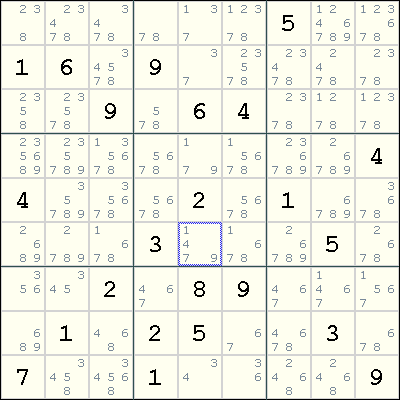
Example

The following example has a Hidden Single for digit 4 at the cell r6c5 (row 6, column 5). This is the only cell with 4 as a candidate in the middle box.

Some Sudoku Helpers, such as SudoCue and Simple Sudoku, have the ability to highlight the cells for a chosen digit. Such highlighting makes Hidden Singles particularly obvious. The following is the same example grid with all cells having 4 as a candidate highlighted.

The six puzzles below can all be solved only using the placement of hidden singles.

1..2..3...2..1..4...3..5..67..6..5...5..8..7...8..4..18..7..4...3..6..2...9..2..7
..1...2.....3.4...5...6...1.5.1.2.7...8...4...2.9.7.8.9...7...8...5.9.....3...7..
1...2...3.4.....1...5.4.6.....2.1...7.8...1.5...4.8.....7.6.8...8.....2.4...3...7
1...2...3.4.....5....6.7.....5...8..7...8...2..6...9.....8.2....1.....6.2...7...1
1..2..3......4..5...6..7..82.....7...5..1..4...7.....98..1..2...6..2......4..6..7
...........12.34...235.617..35...74.....3.....76...82..143.825...87.23...........

See also

• Naked Single

External links

• Hidden Single by Ruud van der Werf
• Forced Digit by Andries E. Brouwer
• Hidden Single by Angus Johnson
• Pinned Square by Kevin Stone
• Hidden Single by Simon Armstrong
• Single-Sqaure Candidate by Paul Stephens
• Hidden Single Number by Gaby Vanhegan
• Single Position by Vincent Tandart
• ExperienceSudoku by Christopher Rucinski