(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
When fish are no longer restricted to rows and columns, strange varieties emerge. When either the defining set or the secondary set contains a mixture of rows, columns and/or boxes, these fish are classified as mutant fish.
There are no mutant X-Wings, because the interaction between a single box and line is fully covered by the Locked Candidates technique.
Here is a fish diagram of a Mutant Swordfish, with the defining set consisting of 2 rows and 1 column, and the secondary set containing 1 column and 2 boxes.
Mutant fish can also be found in finned variations.
The 5 Mutant swordfish patterns
The previous example is the maximum pattern for the mutant swordfish. It consists of 10 cells with 3 group conjugates in rows 1 and 9 and column 7. Fortunately, 4 of the 10 cells in the maximum pattern are redundant. If a candidate is removed from a single cell of any or all of the 4 row and column groups in box 3 and 9, the pattern will still work. Therefore there are 5 patterns for the mutant swordfish with 6, 7, 8, 9, and 10 cells. This is analogous to the 4 patterns of the row or column swordfish with 6, 7. 8. or 9 cells. The maximum pattern is by far the rarest of the 5 patterns.
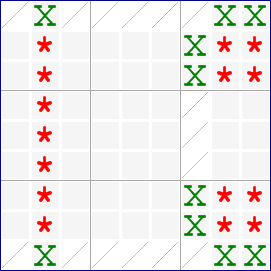
Minimum Pattern for the Mutant Swordfish
The minimum mutant swordfish pattern, which contains only 6 cells is shown in the diagram below. Here all of the group conjugates in the previous example become conjugate pairs.
How it works
There are 3 sets of conjugate pairs in the pattern, AC, BD, and EF. For each of these, one cell must be X and the other must be not X. If A is X, its conjugate C must be not X and there can be no other X in column 2 including B. Therefore B's Conjugate D must be X and and there can be no other X in box 9 including F. Therefore F's conjugate E must be X and there can be no other X in box 3. If B is X, its conjugate D must be not X and there can be no other X in column 2 including A. Therefore A's Conjugate C must be X and and there can be no other X in box 3 including E. Therefore E's conjugate F must be X and there can be no other X in box 9.
A Finned Mutant Swordfish Example
An example of a finned mutant swordfish is shown in the diagram below, The fin appears at r1c7 in box 3. Note this is the only cell where a fin can be located in box 3 since the other cells in box 3 row 1 and column 7 are part of the pattern. The 4 candidate elimination cells also occur in box 3.
See Also
