Common Peer Elimination
Common Peer Elimination is a basic solving technique that primarily applies to Sudoku Variations with irregular groups of cells, such as Jigsaw and Killer Sudoku, and (to a lesser extent) to Sudoku-X. It is based on the following simple principle:
"If a group of cells G is known to contain the digit D, then we can remove D as a candidate from all other cells that can see all candidate positions for digit D in group G."
Note: This technique is a superset of the classical technique Locked Candidates.
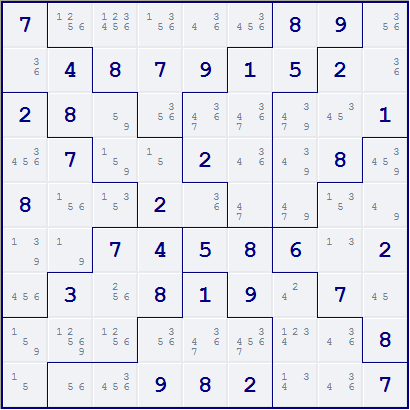
Example 1 (Jigsaw)
The following example is taken from Daily Jigsaw 13. Note that there are three possible positions for the digit 3 in column 9: r1c9, r2c9 and r4c9. All three cells have r4c7 as a common peer. Therefore, the candidate 3 can be eliminated from r4c7.
Example 2 (Killer)
The following example is taken from Weekly Assassin 36. The 27/4 cage at r2c2 must be either {5679} or {4689}, and therefore must contain the digits 6 and 9. Both cells in the 9/2 cage at r1c3 can see all cells in the 27/4 cage. Therefore, the candidate 6 can be eliminated from r12c3, which must therefore contain the digits {27}.
Notes
- If group G (see formal definition above) contains only 2 candidate positions for digit D, the same candidate eliminations can be caught by Simple Coloring.
- For Sudoku-X, Common Peer Elimination catches all simple Crossovers.